Data Strucrures


A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph can be defined as,
A Graph consists of a finite set of vertices(or nodes) and set of Edges which connect a pair of nodes.
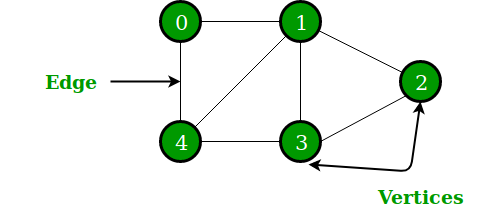
In the above Graph, the set of vertices V = {0,1,2,3,4} and the set of edges E = {01, 12, 23, 34, 04, 14, 13}.
Graphs are used to solve many real-life problems. Graphs are used to represent networks. The networks may include paths in a city or telephone network or circuit network. Graphs are also used in social networks like linkedIn, Facebook. For example, in Facebook, each person is represented with a vertex(or node). Each node is a structure and contains information like person id, name, gender, locale etc.
Graph As an ADT:
Instances:
Graph is a collection of vertices and edges
Operations:
1. total_vertices(): This function returns total number of vertices.
2. total_edges(): This function returns total number of edges.
3. Is_edge(v1,v2): This function returns true if there exists an edge
between v1 and v2.
4. In_degree(): This function returns total number of edges that are
incident to the vertex.
5. Out_degree(): This function returns out degree of the vertex
6. Display(): This function displays the graph in DFS or in BFS
manner
Basic Treminologies:
1. Graph
A graph, G(V,G), consists of two sets V & E i.e. V(G) & E(G). V is a finite non-empty set of vertices. E is a set of pairs of vertices called edges of G
2. Undirected Graph
The edges have no direction in undirected graph G. i.e. the pair(v1,v2) & (v2,v1) represent same edge.
3. Directed Graph
The edges have direction in directed graph G. i.e. the pair <v1, v2> & <v2, v1> represent different edge.
4. Multi Graph
If graph G have multiple occurences of the same edge.
5. Complete Graph
An ‘n’ vertex undirected graph with exactly n( n – 1)/2 edges is said to be complete graph G.
6. Sub Graph
A subgraph of G is a graph G’ such that V(G’) is a subset of V(G) and E(G’) is a subset of E(G).
7. Path
A path from vertex Vp to vertex Vq is a sequence of vertices Vp, Vi1. ..Vq such that (Vp,Vi1),.. . (Vin, Vq) are edges in E(G).
8. Length
The length of a path is the number of edges on it.
9. Simple Path
A simple path is a path in which all vertices except the first and last are distinct.
10. Cycle
A simple path in which the first and last vertices are the same.
11. Degree of Vertex
Number of edges incident to that vertex.
12. Indegree
Number of edges for which vertex ‘V’ is the head.
13. Out Degree
Number of edges for which vertex ‘V’ is the tail.
Applications of Graph
1. Representation of electric circuit
2. Connecting the maps b/w different cities/states/countries.
3. Telephone and computer networks.
4. Constructing road lines from one location to another.
5. Scheduling of independent tasks.
6. For project planning.